無論是小考,高考亦或是中考,平時的學習習慣對于一個學生來說,都至關重要,往往直接決定了考試的成與敗。有人說21天可以養成一個良好的習慣,作為學生的你?能堅持嗎?
1
如何培養高分習慣
提高計算正確率、筆記、考試
1、提高初中數學計算正確率的竅門
真正的去理解解題方法,做完一道題目之后當堂回顧,把解題思路復述出來,并將做錯的題抄在錯題本上,經過一段時間的努力,一定能將解題的錯誤率降低,并養成良好的學習習慣。
所以,我們經常說,學數學很容易,秘訣就是:會做的做對,錯過的不要再錯如何提高中考數學的計算的正確率,以下有四種方法以供借鑒:
第一:要對計算引起足夠的重視
總以為計算式題比分析應用題容易得多,對一些法則、定律等知識學得比較扎實,計算是件輕而易舉的事情,因而在計算時或過于自信,或注意力不能集中,結果錯誤百出。
其實,計算正確并不是一件很容易的事。例如計算一道像37×54這樣簡單的式題,要用到乘法、加法的運算法則,經過四次表內乘法和四次一位數加法才能完成。
至于計算一道分數、小數四則混合運算式題,需要用到運算順序、運算定律和四則運算的法則等大量的知識,經過數十次基本計算。在這個復雜的過程中,稍有粗心大意就會使全題計算錯誤。
因此,計算時來不得半點馬虎。
第二:要按照計算的一般順序進行
首先,弄清題意,看看有沒有簡單方法、得數保留幾位小數等特別要求;
其次,觀察題目特點,看看幾步運算,有無簡便算法;
再次,確定運算順序。在此基礎上利用有關法則、定律進行計算;
最后,要仔細檢查,看有無錯抄、漏抄、算錯現象。
第三:要養成認真演算的好習慣
有些同學由于演算不認真而出現錯誤。數據寫不清,辨認失誤。打草稿時不能按照一定的順序排列豎式,出現上下粘連,左右不分,再加上相同數位不對齊,既不便于檢查,又極易看錯數據。所以一定要養成有序排列豎式,認真書寫數字的良好習慣。
第四:不能盲目追求速度
計算又對又快是最理想的目標,但必須知道計算正確是前提條件,是最基本的要求,沒有正確作基礎的高速度是沒有任何價值的。所以,寧愿計算的速度慢一些,也要保證計算正確,提高計算的正確率。
2、做好數學課堂筆記的五個技巧
首先,要準備一個專門用來記數學筆記的本子。
一個專門的本子非常重要。往往同學們會把老師講課時需要記錄的內容隨手記在書上、或者試卷上,這樣時間久了就容易丟失,想要翻看的時候找起來也很費事,甚至找不到。而有一個專門的筆記本,我們就相當于有了一個移動的存儲器,可以方便、快捷地翻看。
其次,就是如何做好數學筆記。
有的同學在記筆記的時候喜歡把老師寫的每一個字、講的每一句話都記下來,一堂課下來,緊張忙碌不說,勢必會影響你聽課的效果,一堂課只顧著寫了,而沒有認真去思考、理解,到頭來可能是事倍功半。
其實做筆記應掌握以下幾個要點:
第一:記提綱
老師每次上課都會在黑板的左側寫出本節課的提綱,這都是老師上課前準備好的本節課的內容,有了它,可以知道本節課大概都講了什么內容。
第二:記附加
老師在上課的時候有時會加入一些課本沒有的話語,而這些都是對知識的總結,往往也是同學們容易忽視的地方,這些內容可以啟發學生思維的延展性,并且也利于學生基本技能的提升。
第三:記例題
老師每次課上都會有一些比較新穎的例題來為同學們展示,通過例題傳授給學生常用的解題技巧與方法。記錄這些例題,方便同學們對于例題的方法融會貫通,是提高成績的顯著方法。
第四:記疑問
有的同學在課堂上聽老師講課,難免有不明白的地方,但是又怕影響大家上課,而不敢提問,想要課下解決,但是很可能下課就忘記了,這樣疑問就積累下來了,到了最后,越積越多,以至于成績總是不提高。如果能把當時的問題記在筆記本上,這樣在下課的時候即使忘記了,回到家一翻筆記也看到了,這個時候及時問家長或者同學。馬上解決問題是重點,不要把問題留給明天。
第五:記總結
每學完一段知識,一個新的知識,或者學到新的解題方法,都要把自己的心得記錄下來,然后仔細地去咀嚼、去思考:知識的重點在哪里、新的解題方法好在哪里、以后看到類似的問題怎么去運用。有了這樣的思考,那么今后就不會一看到沒見過的題,就擔心自己是否有能力解決,而是考慮這個問題和我學過的哪個知識相關,找到這個題目基本應該用什么樣的方法去解決。形成自己的解題思路,這樣對于提高學生的本身能力是非常有幫助的。
最后:如何利用好數學筆記
數學筆記不能當作一個展示品給別人看,而是要像珍藏品一樣自己時常去看。每天最好給自己安排10分鐘左右的時間把今天所記的筆記認真、仔細地看一遍,鞏固學過的知識。并且在每次的月考、期中、期末前都要認真再看一次,并且把筆記里面的內容前后連結到一起,形成一個知識結果框架,這樣,才能學好數學,提高成績。
3、初中數學考試的5個小技巧
方法一:檢查基本概念
基本概念、法則、公式是同學們檢查時最容易忽視的,因此在解題時極易發生小錯誤而自己卻檢查數次也發現不了,所以,做完試卷第一步,在檢查基本題時,我們要仔細讀題,回到概念的定義中去,對癥下藥。
方法二:對稱檢驗
對稱的條件勢必導致結論的對稱,利用這種對稱原理可以對答案進行快速檢驗。
方法三:不變量檢驗
某些數學問題在變化、變形過程中,其中有的量保持不變,如圖形的平移、旋轉、翻折時,圖形的形狀、大小不變,基本量也不變。利用這種變化過程中的不變量,可以直接驗證某些答案的正確性。
方法四:特殊情形檢驗
問題的特殊情況往往比一般情況更易解決,因此通過特殊值、特例來檢驗答案是非常快捷的方法。
方法五:答案逆推法
相信這種方法很多學生都會,在求出題目的答案后,可將答案重新代回題目中,檢驗題目的條件是否還成立。但是這種方法一定要注意,要想想有沒有可能存在多解的情形。
總而言之,要想提高檢查的次數與效率,又想避免枯燥的重復,就需要一題多解去檢驗。
一道題,使用原來的方法去做,固然也能發現錯誤,但是人都是有慣性思維的,很容易就忽視了一些小的錯誤。
如果在檢查時,我們都盡量去想一些新的方法,那樣,一來可以檢查答案的對錯,二來可以減少機械性重復產生的枯燥感,三來思考新的解法也是鍛煉思維的一種手段,四來能將試卷中的題的作用發揮到最大,可以說是一舉多得的好措施。
此外,直接檢查作為最基礎的方法,要重視技巧直接檢驗法就是圍繞原來的解題方法,針對求解的過程及相關結論進行核對、查校、驗算。為配合檢查,首先應正確使用草稿紙。
建議大家將草稿紙疊出格痕,按順序演算,并標上題號,方便檢查對照。其次,一定要細心細心再細心,每一個細節都需要仔細推敲,而不能“想當然”,記住“最安全的地方有時候也是最危險的地方”。
2
初中數學公式定理大全
111個
乘法與因式分 a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b(a2+ab+b2)
三角不等式 |a+b|≤|a|+|b| |a-b|≤|a|+|b| |a|≤b-b≤a≤b |a-b|≥|a|-|b| -|a|≤a≤|a|
一元二次方程的解 -b+√(b2-4ac)/2a -b-√(b2-4ac)/2a
根與系數的關系 X1+X2=-b/a X1*X2=c/a 注:韋達定理
判別式
b2-4ac=0 注:方程有兩個相等的實根
b2-4ac>0 注:方程有兩個不等的實根
拋物線標準方程 y2=2px y2=-2px x2=2py x2=-2py
直棱柱側面積 S=c*h 斜棱柱側面積 S=c'*h
正棱錐側面積 S=1/2c*h' 正棱臺側面積 S=1/2(c+c')h'
圓臺側面積 S=1/2(c+c')l=pi(R+r)l 球的表面積 S=4pi*r2
圓柱側面積 S=c*h=2pi*h 圓錐側面積 S=1/2*c*l=pi*r*l
弧長公式 l=a*r a是圓心角的弧度數r >0 扇形面積公式 s=1/2*l*r
錐體體積公式 V=1/3*S*H 圓錐體體積公式 V=1/3*pi*r2h
斜棱柱體積 V=S'L 注:其中,S'是直截面面積, L是側棱長
柱體體積公式 V=s*h 圓柱體 V=pi*r2h
常見的初中數學公式
1.過兩點有且只有一條直線
2.兩點之間線段最短
3.同角或等角的補角相等
4.同角或等角的余角相等
5.過一點有且只有一條直線和已知直線垂直
6.直線外一點與直線上各點連接的所有線段中,垂線段最短
7.平行公理 經過直線外一點,有且只有一條直線與這條直線平行
8.如果兩條直線都和第三條直線平行,這兩條直線也互相平行
9.同位角相等,兩直線平行
10.內錯角相等,兩直線平行
11.同旁內角互補,兩直線平行
12.兩直線平行,同位角相等
13.兩直線平行,內錯角相等
14.兩直線平行,同旁內角互補
15.定理 三角形兩邊的和大于第三邊
16.推論 三角形兩邊的差小于第三邊
17.三角形內角和定理 三角形三個內角的和等于180°
18.推論1 直角三角形的兩個銳角互余
19.推論2 三角形的一個外角等于和它不相鄰的兩個內角的和
20.推論3 三角形的一個外角大于任何一個和它不相鄰的內角
21.全等三角形的對應邊、對應角相等
22.邊角邊公理(SAS) 有兩邊和它們的夾角對應相等的兩個三角形全等
23.角邊角公理( ASA)有兩角和它們的夾邊對應相等的兩個三角形全等
24.推論(AAS) 有兩角和其中一角的對邊對應相等的兩個三角形全等
25.邊邊邊公理(SSS) 有三邊對應相等的兩個三角形全等
26.斜邊、直角邊公理(HL) 有斜邊和一條直角邊對應相等的兩個直角三角形全等
27.定理1 在角的平分線上的點到這個角的兩邊的距離相等
28.定理2 到一個角的兩邊的距離相同的點,在這個角的平分線上
29.角的平分線是到角的兩邊距離相等的所有點的集合
30.等腰三角形的性質定理 等腰三角形的兩個底角相等 (即等邊對等角)
31.推論1 等腰三角形頂角的平分線平分底邊并且垂直于底邊
32.等腰三角形的頂角平分線、底邊上的中線和底邊上的高互相重合
33.推論3 等邊三角形的各角都相等,并且每一個角都等于60°
34.等腰三角形的判定定理 如果一個三角形有兩個角相等,那么這兩個角所對的邊也相等(等角對等邊)
35.推論1 三個角都相等的三角形是等邊三角形
36.推論 2 有一個角等于60°的等腰三角形是等邊三角形
37.在直角三角形中,如果一個銳角等于30°那么它所對的直角邊等于斜邊的一半
38.直角三角形斜邊上的中線等于斜邊上的一半
39.定理 線段垂直平分線上的點和這條線段兩個端點的距離相等
40.逆定理 和一條線段兩個端點距離相等的點,在這條線段的垂直平分線上
41.線段的垂直平分線可看作和線段兩端點距離相等的所有點的集合
42.定理1 關于某條直線對稱的兩個圖形是全等形
43.定理 2 如果兩個圖形關于某直線對稱,那么對稱軸是對應點連線的垂直平分線
44.定理3 兩個圖形關于某直線對稱,如果它們的對應線段或延長線相交,那么交點在對稱軸上
45.逆定理 如果兩個圖形的對應點連線被同一條直線垂直平分,那么這兩個圖形關于這條直線對稱
46.勾股定理 直角三角形兩直角邊a、b的平方和、等于斜邊c的平方,即a^2+b^2=c^2
47.勾股定理的逆定理 如果三角形的三邊長a、b、c有關系a^2+b^2=c^2 ,那么這個三角形是直角三角形
48.定理 四邊形的內角和等于360°
49.四邊形的外角和等于360°
50.多邊形內角和定理 n邊形的內角的和等于(n-2)×180°
51.推論 任意多邊的外角和等于360°
52.平行四邊形性質定理1 平行四邊形的對角相等
53.平行四邊形性質定理2 平行四邊形的對邊相等
54.推論 夾在兩條平行線間的平行線段相等
55.平行四邊形性質定理3 平行四邊形的對角線互相平分
56.平行四邊形判定定理1 兩組對角分別相等的四邊形是平行四邊形
57.平行四邊形判定定理2 兩組對邊分別相等的四邊形是平行四邊形
58.平行四邊形判定定理3 對角線互相平分的四邊形是平行四邊形
59.平行四邊形判定定理4 一組對邊平行相等的四邊形是平行四邊形
60.矩形性質定理1 矩形的四個角都是直角
61.矩形性質定理2 矩形的對角線相等
62.矩形判定定理1 有三個角是直角的四邊形是矩形
63.矩形判定定理2 對角線相等的平行四邊形是矩形
64.菱形性質定理1 菱形的四條邊都相等
65.菱形性質定理2 菱形的對角線互相垂直,并且每一條對角線平分一組對角
66.菱形面積=對角線乘積的一半,即S=(a×b)÷2
67.菱形判定定理1 四邊都相等的四邊形是菱形
68.菱形判定定理2 對角線互相垂直的平行四邊形是菱形
69.正方形性質定理1 正方形的四個角都是直角,四條邊都相等
70.正方形性質定理2正方形的兩條對角線相等,并且互相垂直平分,每條對角線平分一組對角
71.定理1 關于中心對稱的兩個圖形是全等的
72.定理2 關于中心對稱的兩個圖形,對稱點連線都經過對稱中心,并且被對稱中心平分
73.逆定理 如果兩個圖形的對應點連線都經過某一點,并且被這一點平分,那么這兩個圖形關于這一點對稱
74.等腰梯形性質定理 等腰梯形在同一底上的兩個角相等
75.等腰梯形的兩條對角線相等
76.等腰梯形判定定理 在同一底上的兩個角相等的梯形是等腰梯形
77.對角線相等的梯形是等腰梯形
78.平行線等分線段定理 如果一組平行線在一條直線上截得的線段相等,那么在其他直線上截得的線段也相等
79.推論1 經過梯形一腰的中點與底平行的直線,必平分另一腰
80.推論2 經過三角形一邊的中點與另一邊平行的直線,必平分第三邊
81.三角形中位線定理 三角形的中位線平行于第三邊,并且等于它的一半
82.梯形中位線定理 梯形的中位線平行于兩底,并且等于兩底和的一半 L=(a+b)÷2 S=L×h
83.(1)比例的基本性質 如果a:b=c:d,那么ad=bc如果ad=bc,那么a:b=c:d
84.(2)合比性質 如果a/b=c/d,那么(a±b)/b=(c±d)/d
85.(3)等比性質 如果a/b=c/d=…=m/n(b+d+…+n≠0),那么 (a+c+…+m)/(b+d+…+n)=a/b
86.平行線分線段成比例定理 三條平行線截兩條直線,所得的對應線段成比例
87.推論 平行于三角形一邊的直線截其他兩邊(或兩邊的延長線),所得的對應線段成比例
88.定理 如果一條直線截三角形的兩邊(或兩邊的延長線)所得的對應線段成比例,那么這條直線平行于三角形的第三邊
89.平行于三角形的一邊,并且和其他兩邊相交的直線,所截得的三角形的三邊與原三角形三邊對應成比例
90.定理 平行于三角形一邊的直線和其他兩邊(或兩邊的延長線)相交,所構成的三角形與原三角形相似
91.相似三角形判定定理1 兩角對應相等,兩三角形相似(ASA)
92.直角三角形被斜邊上的高分成的兩個直角三角形和原三角形相似
93.判定定理2 兩邊對應成比例且夾角相等,兩三角形相似(SAS)
94.判定定理3 三邊對應成比例,兩三角形相似(SSS)
95.定理 如果一個直角三角形的斜邊和一條直角邊與另一個直角三角形的斜邊和一條直角邊對應成比例,那么這兩個直角三角形相似
96.性質定理1 相似三角形對應高的比,對應中線的比與對應角平分線的比都等于相似比
97.性質定理2 相似三角形周長的比等于相似比
98.性質定理3 相似三角形面積的比等于相似比的平方
99.任意銳角的正弦值等于它的余角的余弦值,任意銳角的余弦值等于它的余角的正弦值
100.任意銳角的正切值等于它的余角的余切值,任意銳角的余切值等于它的余角的正切值。
學霸來了
擁有來自清華/北大/復旦/交大等的頂尖名校的學霸師資
為全國中小學分享最有價值的學習經驗
提供真人1對1名師在線輔導
點擊下方“閱讀原文”,報名參加清華北大學霸1對1免費名師測評課!
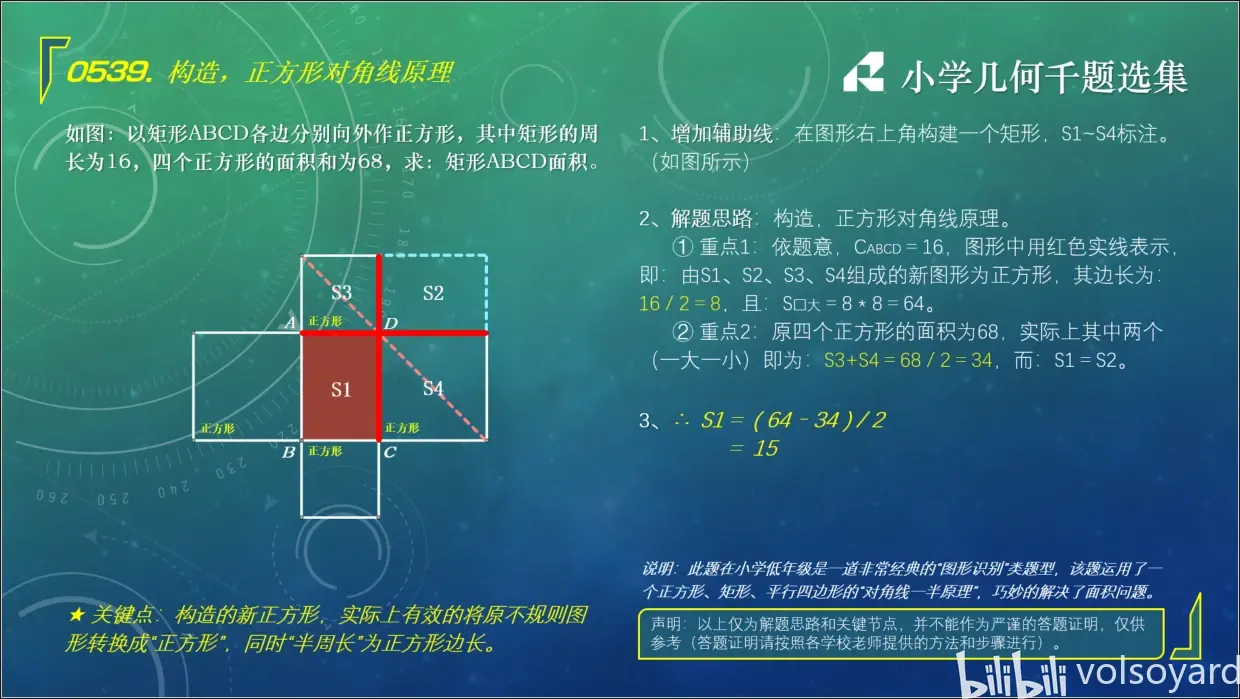
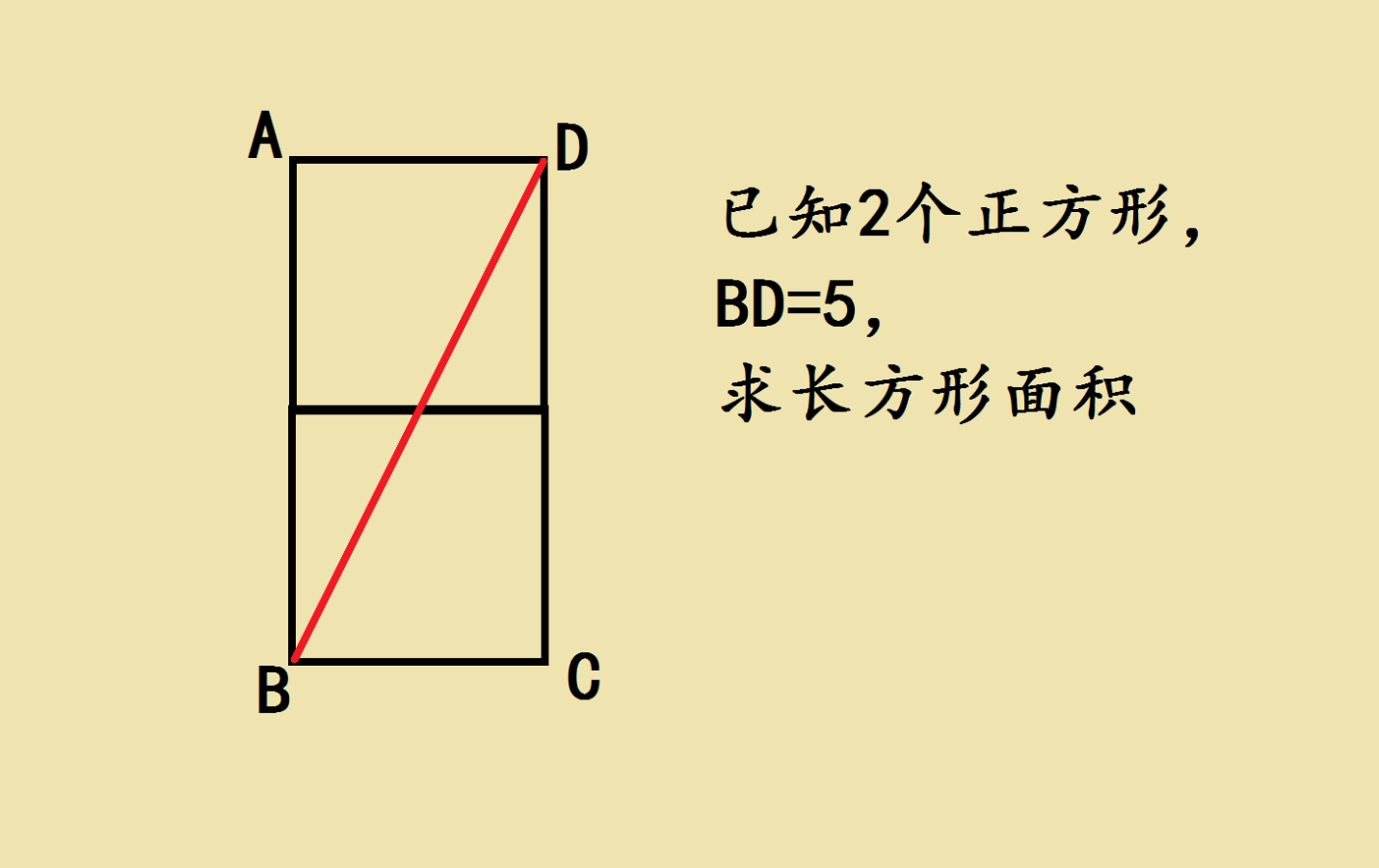
轉載請注明來自夕逆IT,本文標題:《正方形對角線最笨算法》

 京公網安備11000000000001號
京公網安備11000000000001號 京ICP備11000001號
京ICP備11000001號
還沒有評論,來說兩句吧...